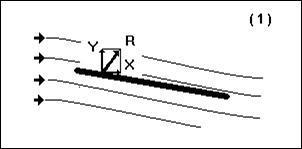
Тема №2: Силы, действующие на крыло СЛА. Основные характеристики крыла, графики и поляры.
Полная аэродинамическая сила.
Согласно третьему закону Ньютона сила воздействия крыла на воздух равна силе воздействия воздушного потока на крыло. Эта сила получила название полной аэродинамической силы R крыла.
Полная аэродинамическая сила – это сила, с которой набегающий воздушный поток воздействует на твердое тело.
Центр давления – точка приложения этой силы.
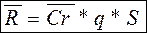
- R - Полная аэродинамическая сила.
- Cr - Коэффициент полной аэродинамической силы.
- q - Динамический напор.
- S - Эффективная площадь тела.
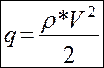
- r - Плотность воздуха.
- V - Скорость тела относительно воздуха (или «воздушная скорость» тела).
Сила воздействия воздушного потока на твердое тело зависит от многих параметров, главными из которых являются форма и ориентация тела в потоке, линейные размеры тела и интенсивность воздушного потока, определяющаяся его плотностью и скоростью.
Из формулы видно, что сила воздействия воздушного потока на тело зависит от линейных размеров тела, интенсивности воздушного потока, которая определяется его плотностью и скоростью, и коэффициента полной аэродинамической силы Cr.
Наибольший интерес в этой формуле представляет коэффициент Cr, определяющийся множеством факторов, главными из которых являются форма тела и его ориентацией в воздушном потоке. Аэродинамика – наука экспериментальная. Формул, позволяющих абсолютно точно описать процесс взаимодействия твердого тела с набегающим потоком воздуха, пока нет. Однако было замечено, что тела, имеющие одинаковую форму (при разных линейных размерах), взаимодействуют с воздушным потоком одинаково. Можно сказать, что Cr = R (полной аэродинамической силе) при продувке тела некоторого единичного размера воздушным потоком единичной интенсивности. Такого рода коэффициенты очень широко используются в аэродинамике, так как они позволяют исследовать характеристики летательных аппаратов (ЛА) на их уменьшенных моделях.
При взаимодействии твердого тела с потоком воздуха неважно, движется ли тело в неподвижном воздухе или неподвижное тело обтекается движущимся воздушным потоком. Возникающие силы взаимодействия будут одинаковы. Но, с точки зрения удобства изучения этих сил, проще иметь дело со вторым случаем.
Для удобства выполнения аэродинамических расчетов полную аэродинамическую силу R можно разложить на три взаимно перпендикулярные составляющие в скоростной системе координат. Положительное направление оси X будет направлено по вектору скорости полета, оси Y перпендикулярно к оси X вверх, а ось Z направлена перпендикулярно к плоскости, в которой находятся оси X и Y. Составляющую полной аэродинамической силы вдоль оси X назвали силой аэродинамического сопротивления. Составляющую вдоль оси Y – подъемной силой.
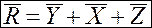
- R - Полная аэродинамическая сила.
- Y - Подъемная сила.
- X - Сила лобового сопротивления.
- Z - Боковая сила.
Формулы подъемной силы и силы сопротивления очень похожи на формулу полной аэродинамической силы. Что неудивительно, так как и Y, и X являются составными частями R.
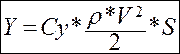
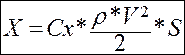
- Cy - Коэффициент подъемной силы.
- Cx - Коэффициент сопротивления.
- r - Плотность воздуха.
- V - Скорость тела относительно воздуха (воздушная скорость).
- S - Эффективная площадь тела.
Зависимость сил, действующих на крыло от угла атаки. Графики зависимости сил действующих на крыло от угла атаки.
Ранее уже говорилось о том, что величина и направление действия аэродинамической силы зависят от формы обтекаемого тела и его ориентации в потоке. Зависимость сил, действующих на крыло проще всего рассмотреть на примере пластинки, обтекаемой воздушным потоком.
Если установить пластину вдоль потока (угол атаки нуль), то обтекание будет симметричным (рис. 1, положение 0). В этом случае поток воздуха пластиной не отклоняется и подъемная сила Y равна нулю. Сопротивление X минимально, но не нуль. Оно будет создаваться силами трения молекул воздуха о поверхность пластины. Полная аэродинамическая сила R минимальна и совпадает с силой сопротивления X.
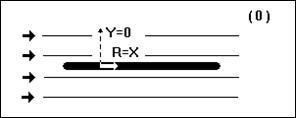
Рис. 1. Пластина установлена вдоль потока
Начнем понемногу отклонять пластину. Из-за скашивания потока сразу же появляется подъемная сила Y. Сопротивление X немного увеличивается из-за увеличения поперечного сечения пластины по отношению к потоку.
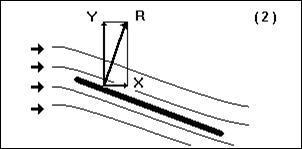
По мере постепенного увеличения угла атаки и увеличения скоса потока подъемная сила увеличивается. Очевидно, что сопротивление тоже растет. Здесь необходимо отметить, что на малых углах атаки подъемная сила растет значительно быстрее, чем сопротивление (рис. 2 и 3, положения 1 и 2).
|
|
 |
|
Рис. 2. Начало отклонения пластины |
Рис. 3. Увеличиваем отклонение пластины |
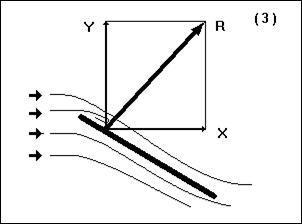
По мере увеличения угла атаки воздушному потоку становится все труднее обтекать пластину. Подъемная сила хотя и продолжает увеличиваться, но медленнее, чем раньше. А вот сопротивление растет все быстрее и быстрее, постепенно обгоняя рост подъемной силы. В результате полная аэродинамическая сила R начинает отклоняется назад (рис. 4, положение 3).
И тут вдруг картина резко меняется. Воздушные струйки оказываются не в состоянии плавно обтекать верхнюю поверхность пластины. За пластиной образуется мощный вихрь. Подъемная сила резко падает, а сопротивление увеличивается. Это явление в аэродинамике называют срыв потока. «Сорванное» крыло перестает быть крылом. Оно перестает лететь и начинает падать (рис. 5, положение 4).
 |
 |
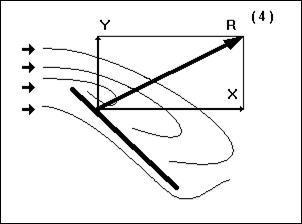| Рис. 4. Полная аэродинамическая сила отклоняется назад | Рис. 5. Срыв потока |
Поляра Лилиенталя 1-го рода.
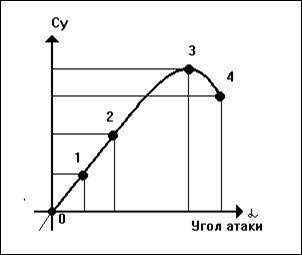
Покажем зависимость коэффициентов подъемной силы Cy и сопротивления Cx от угла установки пластины к набегающему потоку (угла атаки) на графиках (рис. 6 и 7). Для этого на каждом из них по горизонтальной оси будем откладывать величины угла атаки в градусах, а по вертикальной - длины векторов Су и Сх, получающиеся при положениях 1-4 пластины на предыдущих графиках.
 |
 |
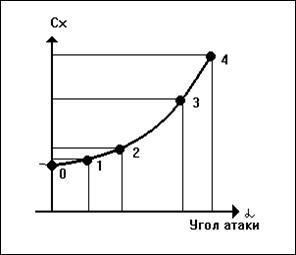| Рис. 6. Зависимость коэффициента подъемной силы Cy от угла атаки | Рис. 7. Зависимость коэффициента сопротивления Cx от угла атаки |
Объединим получившиеся два графика в один. По оси X отложим значения коэффициента сопротивления Cx, а по оси Y коэффициент подъемной силы Cy (рис. 8). Значения коээфициентов соответствуют длинам векторов Сх и Су на предыдущих графиках при положениях пластины 1-4.
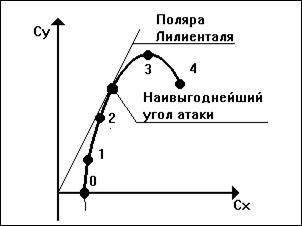
Рис. 8. Поляра крыла (поляра Лилиенталя 1-го рода)
Получившаяся кривая называется поляра крыла или поляра Лилиенталя 1-го рода. Это основной график, характеризующий летные свойства крыла - график, показывающий зависимость коэффициентов подъемной силы и сопротивления от угла атаки крыла.
Откладывая на осях координат значения коэффициентов подъемной силы Cy и сопротивления Cx, этот график показывает величину и направление действия полной аэродинамической силы R. Если считать, что воздушный поток движется вдоль оси Cx слева направо, а центр давления (точка приложения полной аэродинамической силы) находится в центре координат, то для каждого из разобранных ранее углов атаки вектор полной аэродинамической силы будет идти из начала координат в точку поляры, соответствующую заданному углу атаки. На поляре можно легко отметить три характерные точки и соответствующие им углы атаки: критический, экономический и наивыгоднейший.
Критический угол атаки – это угол атаки, при превышении которого происходит срыв потока (между точками 3 и 4 на графике). Критический угол атаки интересен тем, что при выходе на него крыло летит с минимальной скоростью. Условием прямолинейного полета с постоянной скоростью является равновесие между полной аэродинамической силой и силой тяжести.
Вспомним формулу полной аэродинамической силы:
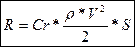
Из формулы видно, что для обеспечения постоянности итогового значения аэродинамической силы R увеличение коэффициента Cr неизбежно ведет к уменьшению скорости полета V, так как значения плотности воздуха r и площади крыла S остаются неизменными.
Экономический угол атаки – это угол атаки, на котором аэродинамическое сопротивление крыла минимально (между точками 1 и 2 на графике). Если установить крыло на экономический угол атаки, то оно сможет двигаться с максимальной скоростью.
Наивыгоднейший угол атаки – это угол атаки, на котором отношение коэффициентов подъемной силы и сопротивления Cy/Cx максимально (между точками 2 и 3 на графике). В этом случае угол отклонения аэродинамической силы от направления движения воздушного потока максимален. При установке крыла на наивыгоднейший угол атаки оно полетит дальше всего.
Полное лобовое сопротивление СЛА.
Мы уже говорили, что при увеличении угла атаки крыла коэффициент подъемной силы Cy сначала возрастает от 0, а затем, при достижении какого-то максимального значения, с дальнейшем увеличением угла атаки начинает уменьшаться (рис. 6).
В свою очередь, у силы лобового сопротивления нулевого значения нет (рис. 7). Сила лобового сопротивления есть при любом угле атаки и направлена всегда против движения крыла. Это объясняется тем, что лобовое сопротивление крыла является суммой сил, вызываемых различными причинами и действующих в разных режимах полета.
Профильное сопротивление крыла.
Сопротивление крыла бесконечного размаха называется профильным сопротивлением и обозначается Qp. Профильное сопротивление, вызываемое разностью давлений перед крылом и за ним, а также трением воздуха о его поверхность в пограничном слое, зависит только от формы профиля и шероховатости поверхности крыла:
,
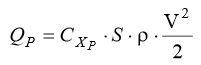- где Сxp - коэффициент профильного сопротивления.
Пограничный слой (ПС) – это тонкий слой воздуха, непосредственно примыкающий к обтекаемой поверхности и тормозящийся о нее.
Непосредственно на обтекаемой поверхности скорость потока равна нулю. В этом легко убедиться. Вспомните, например, крылья бабочек. Они покрыты тончайшей пыльцой, которая не сдувается набегающим потоком.
По мере удаления от поверхности тела ее влияние на поток уменьшается, и скорость потока, соответственно, увеличивается. Толщина пограничного слоя для сверхлегких летательных аппаратов (СЛА) составляет 2-12 мм. Различают ламинарный (ровный) и турбулентный (вихревой) пограничные слои (рис. 9).
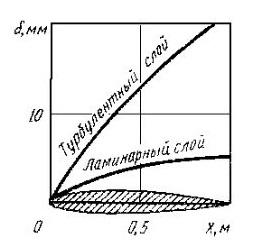
Рис. 9. Пограничный слой
Ламинарный ПС встречается на очень гладких поверхностях обтекания, как правило, при малых скоростях и температурах набегающего потока. По мере удаления от передней кромки толщина пограничного слоя увеличивается, и он из ламинарного обычно превращается в турбулентный. На парапланах и дельтапланах из-за шершавости материала, из которого изготовлены крылья, пограничный слой практически всегда турбулентный. При увеличении толщины пограничного слоя до некоторого критического значения происходит его отрыв от обтекаемой поверхности (рис. 10).
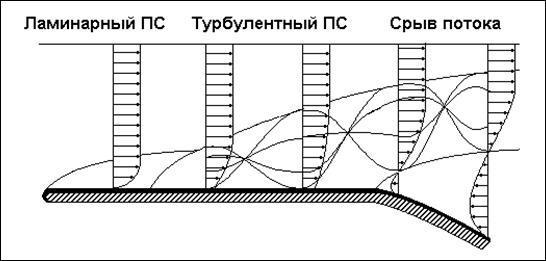
Рис. 10. Отрыв пограничного слоя
Обсуждавшийся ранее «срыв потока» фактически определяется отрывом пограничного слоя.
Индуктивное сопротивление крыла.
Второй составляющей полного лобового сопротивления крыла является индуктивное сопротивление. При переходе от крыла бесконечного размаха к крылу конечного удлинения появляется новый вид сопротивления, величина которого резко повышается при увеличении угла атаки. Это сопротивление называется индуктивным и обозначается Qi.
,
-
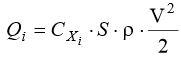где
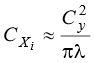- коэффициент индуктивного сопротивления, зависящий от удлинения крыла и угла атаки.
Индуктивное сопротивление объясняется перетеканием воздуха по торцам крыла из области повышенного давления в область пониженного давления над крылом (рис. 11). Так как разность давления на поверхности крыла определяет величину подъемной силы, то между подъемной силой и индуктивным сопротивлением имеется тесная связь. Если нет подъемной силы, индуктивное сопротивление отсутствует. Чем больше угол атаки, тем больше подъемная сила и, следовательно, индуктивное сопротивление.
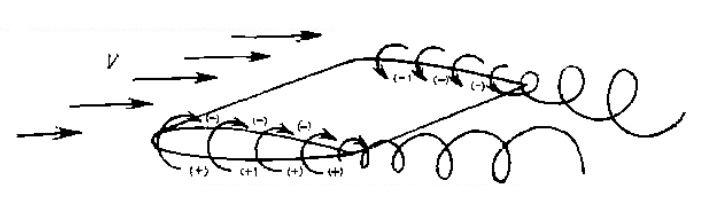
Рис. 11. Перетекание воздуха по торцам крыла
Таким образом, полное лобовое сопротивление крыла в общем случае складывается из профильного и индуктивного сопротивлений (мы обозначали его буковкой Х, как ось, по которой оно направлено, но вообще-то его обозначают буковкой Q).
Q = Qp + Qi
На малых углах атаки основной частью лобового сопротивления является профильное. По мере увеличения угла атаки сопротивления в общем сопротивлении крыла уменьшается, а доля индуктивного - возрастает и на больших углах атаки составляет основную часть лобового сопротивления.
Основные параметры, характеризующие форму крыла. Профилированное крыло.
Существует бесчисленное множество форм крыльев. Это объясняется тем, что каждое крыло рассчитывается под совершенно определенные режимы полета, скорости, высоты. Поэтому выделить какую-то оптимальную или «наилучшую» форму невозможно. Каждое хорошо работает в «своей» области применения. Обычно форму крыла определяют, задавая профиль, вид в плане, угол крутки и угол поперечного V. Разберем эти понятия.
Профиль крыла - форма (контур) сечения крыла плоскостью, параллельной плоскости симметрии крыла (рис. 12).
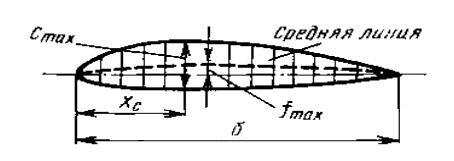
Рис. 12. Профиль крыла
Существует огромное количество видов профилей крыла, отвечающих тем или иным режимам полёта. Вот, к примеру (рис. 13):
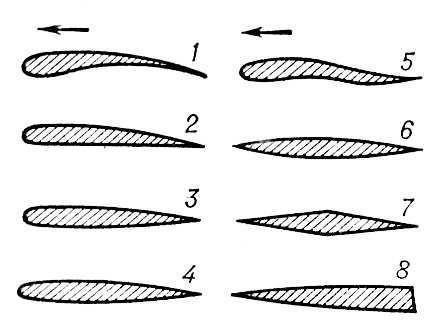
Рис. 13. Виды профилей крыла: 1 — вогнуто-выпуклый; 2 — плоско-выпуклый; 3 — двояковыпуклый несимметричный; 4 — двояковыпуклый симметричный; 5 — S-oбразный (используется в конструкции дельтаплана); 6 — чечевицеобразный; 7 — ромбический; 8 — клиновидный. Стрелкой показано направление полёта.
Описывая форму профиля, применяют прямоугольную систему координат с началом в передней точке хорды. Ось X направляют по хорде от передней точки к задней, а ось Y - вверх (от нижней границы профиля к верхней). Границы профиля задаются по точкам с помощью таблицы или формулами. Контур профиля строят также, задавая среднюю линию и распределение толщины профиля вдоль хорды.
Основными параметрами, характеризующими форму профиля крыла, являются (рис. 11):
Относительная толщина профиля (С) - отношение максимальной толщины профиля Сmax к его хорде b, измеряемое в процентах.
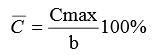
Хорда профиля - отрезок, соединяющий наиболее удаленные точки профиля. Длину хорды обозначают через b (как у нас на рисунках 11 и 13).
Координата Хс максимальной толщины профиля измеряется в процентах от хорды, считая от носка профиля:
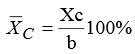
Максимальная относительная кривизна (вогнутость) профиля ( f ) - отношение максимальной стрелы прогиба средней линии профиля fmax к его хорде, измеряемое в процентах:
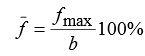
Иначе говоря, кривизна профиля – это кривизна его средний линии. Кривизну профиля принято характеризовать вогнутостью профиля, определяемой стрелой прогиба средний линии профиля.
Стрелой перегиба называется максимальное отклонение средней линии профиля от его хорды.
Средней линией профиля называется линия, проходящая через середины отрезков, соединяющих точки с одинаковой координатой X на верхнем и нижнем обводах профиля.
Кривизна профиля считается положительной, если средняя линия лежит выше хорды. При этом, вогнутость профиля может изменяться по хорде и даже менять знак для профилей с S-образной средний линией (как у наших дельтапланов).
Закон Бернулли и профилированное крыло.
При дозвуковых скоростях полёта положительная вогнутость профиля создаёт не зависящие от угла атаки приращения коэффициента подъёмной силы Сy за счет дополнительного торможения потока нижней частью профиля. Иными словами, вогнутый «ковшик» профиля (как на рис. 12) притормаживает поток воздуха снизу, независимо от угла атаки всего профиля. А по закону Бернулли: чем ниже скорость, тем выше давление. Таким образом, происходит дополнительное увеличение давления воздуха под крылом, подъемная сила увеличивается.
Геометрические характеристики дельтаплана.
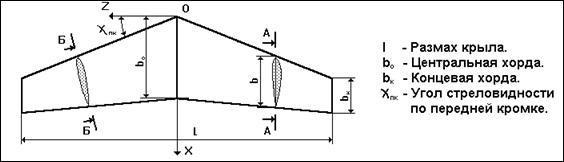
Рис. 14. Вид крыла в плане
Описывая форму крыла, используют следующие понятия (рис. 14):
Размах крыла - расстояние между плоскостями, параллельными плоскости симметрии и касающимися концов крыла.
Местная хорда - хорда профиля в произвольном сечении Z.
Центральная хорда - местная хорда в плоскости симметрии.
Концевая хорда - хорда в концевом сечении.
Если концы крыла закруглены, то концевая хорда определяется так, как это показано на рисунке 15.
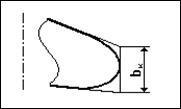
Рис. 15. Определение концевой хорды у крыла с закругленной законцовкой
Площадь крыла - площадь проекции крыла в плане или площадь проекции крыла на его базовую плоскость. Под базовой плоскостью мы будем понимать плоскость, содержащую центральную хорду и перпендикулярную плоскости симметрии крыла.
Угол стреловидности по передней кромке - угол между касательной к линии передней кромки и плоскостью, перпендикулярной центральной хорде.
Местный угол крутки - угол между проекцией на плоскость, перпендикулярную центральной хорде, касательной к линии 1/4 хорд и базовой плоскостью крыла (рис. 14/2).
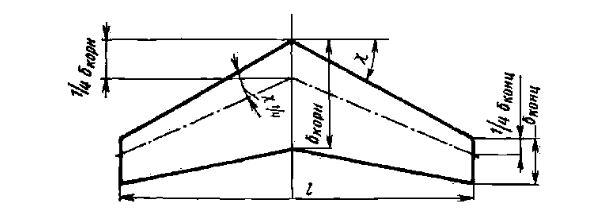
Рис. 14/2. Вид крыла в плане
Геометрическая крутка закладывается при проектировании ЛА и заключается в изменении углов атаки профилей разных сечений крыла (местных углов крутки). Сам профиль при этом сохраняет одинаковую форму (рис. 16).
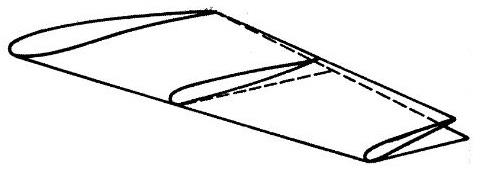
Рис. 16. Геометрическая крутка крыла
Аэродинамическая крутка – это изменение формы профилей сечений крыла по всему размаху при одинаковых углах атаки профилей (рис. 17).
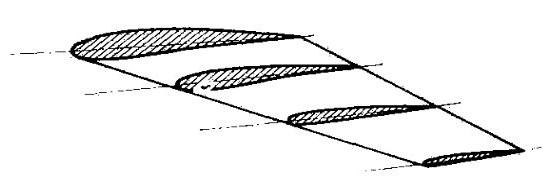
Рис. 17. Аэрдинамическая крутка крыла
Крутка считается положительной, если координата Y передней точки хорды больше координаты Y задней точки хорды. Если наоборот, координата Y передней точки хорды меньше координаты задней – крутка считается отрицательной.
Наличие крутки приводит к тому, что отдельные участки крыла устанавливаются к воздушному потоку под разными углами атаки. А это, в свою очередь, расширяет диапазон рабочих углов атаки крыла.
Местный угол поперечного V-образия крыла - угол между плоскостью хорд крыла и базовой плоскостью крыла (рис. 18).
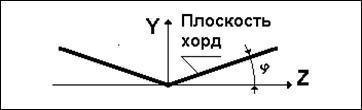
Рис. 18. Угол поперечного V крыла
Форма трапециевидных крыльев определяется тремя параметрами:
Удлинение крыла - отношение квадрата размаха к площади крыла.
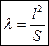
Сужение крыла - отношение длин центральной и концевой хорд.
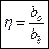
Угол стреловидности по передней кромке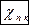 
- угол между касательной к линии передней кромки и плоскостью, перпендикулярной центральной хорде. В зависимости от величины и знака угла стреловидности различают ряд форм трапециевидных крыльев (рис. 19):
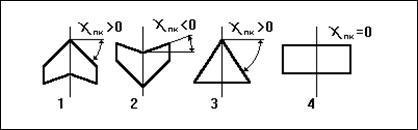
Рис. 19. Формы трапециевидных крыльев.
1 – стреловидное крыло. 2 – обратной стреловидности. 3 – треугольное. 4 – нестреловидное